ML(머신러닝) :: Gradient Descent(경사하강법)
- Soojin Woo

- 2020년 4월 28일
- 2분 분량
최종 수정일: 2020년 5월 13일
Contents in the post based on the free Coursera Machine Learning course, taught by Andrew Ng.
To plot out every point, and read off the numbers manually is not a recommended way.
So we will learn about the 'Gradient Descent' algorithm that automatically finds out the value of θ0 and θ1, which minimize the Cost Function J.
1. What is the Gradient Descent Algorithm?
Gradient Descent is an algorithm that is used to minimize the Cost Function.
But it is not only used for 'linear regression' problems. Gradient Descent is applied to solve more general problems like the Minimization of J(θ0, ...,θn).
2. Outline of Gradient Descent
① Starts with some θ0 and θ1.
// Firstly, we have to assume the initial value of θ0 and θ1. Generally, it is initialized with 0.
② Keep changing θ0 and θ1 to reduce J(θ0, θ1) until we hopefully end up at a minimum.
// To reduce the J(θ0, θ1), we have to gradually change the value of θ0 and θ1.
Take a baby step to go down the hill as rapidly as possible until converge to each local minimum.
3. Simultaneous update

You should repeat it until convergence. But you should have to beware of 'Simultaneous' update.
Correct: Simultaneous update Incorrect
4. Learning rate & Derivative
α: learning rate


- Case 1) Function has a positive derivative


In the case of, the function has a positive derivative, θ1 := θ1-α(positive). Therefore it moves towards left side.
- Case 2) Function has a negative derivative

On the other hand, if the function has a negative slope, then θ1 := θ1-α(negative). So it moves towards the right side.
5. Gradient descent for Linear regression with one variable.

To apply gradient descent, we have to use a differential coefficient.
Below equations are Gradient Descent algorithm which is used in the Linear regression.


In Linear regression, Gradient Descent of Cost Function always converges to the global optimum.


And we could also know that depend on initial points, we could end up at different local optima.









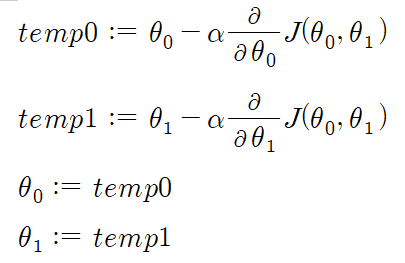

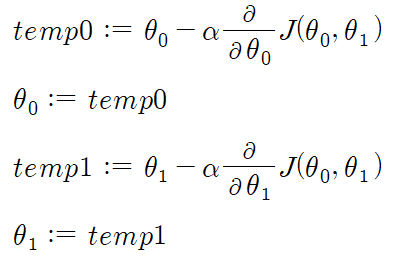



댓글